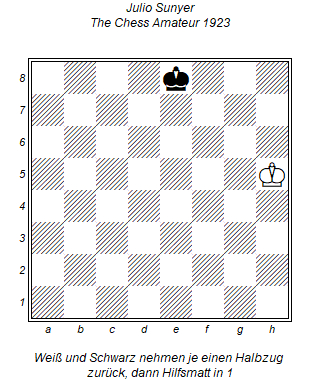
Eine berühmte und vielfach nachgedruckte Aufgabe des spanischen Komponisten Julio Sunyer (1888-1957). Weiß und Schwarz nehmen jeweils ihren letzten Halbzug zurück, danach steht ein Hilfsmatt in 1 auf dem Brett; das heißt, Schwarz macht einen Halbzug und Weiß kann anschließend mattsetzen.
Im Wettkampfschach hatte Julio Sunyer offenbar eine unerwiderte Liebe zur Orang-Utan-Eröffnung.
9 Kommentare
Stimmt, die Aufgabe ist sehr bekannt. Ich muss mich daher als potentiellen Löser selbst disqualifizieren. (Ich meine, ich hätte sie in einem Band der Schachkuriositäten von Krabbé gesehen. Ich kann aber schlecht das Thema des Kapitels nennen, in dem ich sie vermute, das wäre nämlich ein ähnlich starker Hinweis wie „Eckspringer“.) Also viel Erfolg bei der Suche denen, die die Aufgabe noch nicht kennen.
Ich habe mal die Schlagwörter ergänzt, um die Lösung zu erleichtern.
Na ja, ich hätte als ersten Hinweis den Tipp gegeben, dass die gespiegelte Stellung Ka5 und Kd8 nicht lösbar ist…
Wenn ein schwarzer König auf e8 steht, gehen doch ohnehin alle Alarmlämpchen des Problemfreundes an!
Ich glaube ich hab es. Trotz des Winks mit dem Zaunpfahl war das eine schwere Geburt. Bei dieser Art von Aufgabe muss man eine ziemlich wilde Phantasie haben. Weiß nimmt Kg6xTh5 zurück, Schwarz Th8xDh5. Nun könnte schwarz klein röcheln (im wahrsten Sinne des Wortes) und Weiß Dh5-h7# spielen und dem Schabernack ein Ende bereiten.
Ich konnte es auch nur mit dem Schlagwort „Rochade“ lösen, der König auf e8 war für mich zunächst überhaupt nicht verdächtig. Und selbst danach störten noch Probleme wie
1) auf h5 kann keine weiße Dame sein, dann steht nämlich der Ke8 im Schach und darf nicht rochieren
2) ein weißer Turm auf h5 kann irgendwie nicht direkt mattsetzen
Es ist ähnlich wie bei den Spielstärken auf der Schacholympiade: es gibt hier ein enormes Problemlösestärkegefälle von MiBu und Stefan bis zu Alex und LowScore! :-)
Naja, ich bin beim Lösen natürlich ein bisschen im Vorteil, weil ich die Lösung schon kenne :)
Kann ich bestätigen, bei Kenntnis der Lösung genügt ein flüchtiger Blick aufs Diagramm. Das erwähnte Kapitel in Krabbés Büchlein beschäftigt sich natürlich mit der Rochade.
PS: Ich habe das Büchlein (Schach-Bbesonderheiten Band 1) gerade noch mal zur Hand genommen, in der Tat ist dort diese Aufgabe auf Seite 37 abgedruckt.