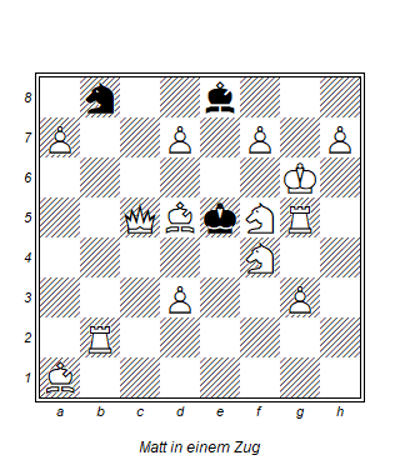
Beim Durchblättern meines allersten Schachbuchs bin ich hierauf gestoßen:
Die Aufgabenstellung ist stark nebenlösig. Was im Normalfall im Problemschach ein K.O.-Kriterium ist, ist hier die Aufgabe: Auf wieviele verschiedene Arten kann Weiß mattsetzen? Wer also auf der Suche nach Kontemplation ist oder abends nicht einschlafen kann, kann hier die Lösungszüge (statt Schäfchen) zählen. Der Autor war in meinem Buch leider nicht angegeben. Kann jemand helfen?
6 Kommentare
Das wird eine lange Liste:
2: axbD/L#
14: Ta2/b1/b3/b4/b5/b6/b7/xb8/c2/d2/e2/f2/g2/h2#
6: Dc3/c7/d4/d6/e3/e7#
1: d4#
11: La2/a8/b3/b7/c4/c6/e4/e6/f3/g2/h1#
2: dxe8D/T#
7: Sd4/d6/e3/e7/g7/h4/h6#
2: fxe8D/T#
2: h8D/L#
Immerhin bleiben noch 44 andere Zugmöglichkeiten, also die Chance auf ein Zufallsmatt ist hier in etwa fifty-fifty.
Zur Quelle habe ich keine Infos. Die Aufgabe wurde vor zwei Monaten bei der HSG Stralsund gepostet, vielleicht weiß dort jemand Bescheid?
Danke für die richtige Lösung. Ich könnte mir vorstellen, dass das auch das Maximum darstellt.
Aufgabe 12 unter dem Stralsunder Link ist auch sehr originell.
Wobei die Aufgabe dort nicht exakt formuliert ist.
Hallo Stefan, ich habe auf schemingmind eine Pyramidenpartie mit Dir begonnen in Shatranj.
Bist Du dort noch aktiv?
Mit lieben Grüßen
Jetzt wieder :)